#JustRandomBlog: January 2019

1. Pengertian Jaringan Syaraf Tiruan

Jaringan syaraf tiruan (artifical neural network) adalah sistem komputasi yang arsitektur dan operasinya diilhami dari pengetahuan tentang sel syaraf biologis di dalam otak. Jaringan syaraf tiruan merupakan salah satu representasi buatan dari otak manusia yang selalu mencoba menstimulasi proses pembelajaran pada otak manusia tersebut. Jaringan syaraf tiruan dapat digambarkan sebagai model matematis dan komputasi untuk fungsi aproksimasi non-linear, klasifikasi data cluster dan regresi non-parametrik atau sebuah simulasi dari koleksi model jaringan syaraf biologi.

Model jaringan syaraf ditunjukkan dengan kemampuannya dalam emulasi, analisis, prediksi dan asosiasi. Kemampuan yang dimiliki jaringan syaraf tiruan dapat digunakan untuk belajar dan menghasilkan aturan atau operasi dari beberapa contoh atau input yang dimasukkan dan membuat prediksi tentang kemungkinan output yang akan muncul atau menyimpan karakteristik input yang diberikan kepada jaringan syaraf tiruan.

Salah satu organisasi yang sering digunakan dalam paradigma jaringan syaraf tiruan adalah perambatan galat mundur atau backpropagation. (Hermawan, 2006)

2. Konsep Dasar Jaringan Syaraf Tiruan

Jaringan syaraf tiruan terdiri dari beberapa neuron dan ada hubungan antar neuron- neuron seperti pada otak manusia. Neuron/selsaraf adalah sebuah unit pemroses informasi yang merupakan dasar operasi jaringan syaraf tiruan.

Jaringan syaraf tiruan terdiri atas beberapa elemen penghitung tak linier yang masing-masing dihubungkan melalui suatu pembobot dan tersusun secara paralel. Pembobot inilah yang nantinya akan berubah (beradaptasi) selama proses pelatihan.

Pelatihan perlu dilakukan pada suatu jaringan syaraf tiruan sebelum digunakan untuk menyelesaikan masalah. Hasil pelatihan jaringan syaraf tiruan dapat diperoleh tanggapa yang benar (yang diinginkan) terhadap masukan yang diberikan. Jaringan syaraf tiruan dapat memberikan tanggapan yang benar walaupun masukan yang diberikan terkena derau atau berubah oleh suatu keadaan. (Hermawan, 2006)

1. Pengertian Jaringan Syaraf Tiruan

Salah satu organisasi yang sering digunakan dalam paradigma jaringan syaraf tiruan adalah perambatan galat mundur atau backpropagation. (Hermawan, 2006)

2. Konsep Dasar Jaringan Syaraf Tiruan

3. Karakteristik Jaringan Syaraf Tiruan

Penyelesaian masalah dengan jaringan syaraf tiruan tidak memerlukan pemrograman. Jaringan syaraf tiruan menyelesaikan masalah melalui proses belajar dari contoh-contoh pelatihan yang diberikan. Biasanya pada jaringan syaraf tiruan diberikan sebuah himpunan pola pelatihan yang terdiri dari sekumpulan contoh pola. Proses belajar jaringan syaraf tiruan berasal dari serangkaian contoh-contoh pola yang diberikan.metode pelatihan yang sering dipakai adalah metode belajar terbimbing. Selama proses belajar itu pola masukan disajikan bersama-sama dengan pola keluaran yang diinginkan. Jaringan akan menyesuaikan nilai bobotnya sebagai tanggapan atas pola masukan dan sasaran yang disajikan tersebut. (Hermawan, 2006)

3.1. Faktor Bobot

Bobot merupakan suatu nilai yang mendefinisikan tingkat atau kepentingan hubungan antara suatu node dengan node yang lain. Semakin besar bobot suatu hubungan menandakan semakin pentingnya hubungan kedua node tersebut.

Bobot merupakan suatu hubungan berupa bilangan real maupun integer, tergantung dari jenis permasalahan dan model yang digunakan. Bobot-bobot tersebut bisa ditentukan untuk berada didalam interval tertentu. selama proses pelatihan, bobot tersebut dapat menyesuaikan dengan pola-pola input.

Jaringan dengan sendirinya akan memperbaiki diri terus-menerus karena adanya kemampuan untuk belajar. Setiap ada suatu masalah baru, jaringan dapat belajar dari masalah baru tersebut, yaitu dengan mengatur kembali nilai bobot untuk menyesuaikan karakter nilai. (Puspaningrum, 2006)

3.2. Fungsi Aktivasi

Setiap neuron mempunyai keadaan internal yang disebut level aktivasi atau level aktivitas yang merupakan fungsi input yang diterima. Secara tipikal suatu neuron mengirimkan aktivitasnya kebeberapa neuron lain sebagai sinyal. Yang perlu diperhatikan adalah bahwa neuron hanya dapat mengirimkan satu sinyal sesaat, walaupun sinyal tersebut dapat dipancarkan ke beberapa neuron yang lain.

Ada beberapa pilihan fungsi aktivasi yang digunakan dalam metode backpropagation, seperti fungsi sigmoid biner, dan sigmoid bipolar. Karakteristik yang harus dimiliki fungsi fungsi aktivasi tersebut adalah kontinue, diferensiabel, dan tidak menurun secara monoton. Fungsi aktivasi diharapkan dapat mendekati nilai-nilai maksimum dan minimum secara baik. Berikut ini adalah fungsi aktivasi yang sering digunakan yaitu: (Puspaningrum, 2006)

Fungsi Sigmoid Biner

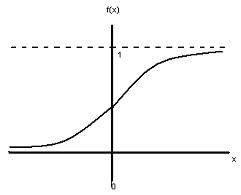
Fungsi ini digunakan untuk jaringan syaraf yang dilatih dengan menggunakan metode backpropagation. Fungsi sigmoid biner memiliki nilai pada range 0 sampai 1. Fungsi ini sering digunakan untuk jaringan syaraf yang membutuhkan nilai output yang terletak pada interval 0 sampai 1. Definisi fungsi sigmoid biner adalah segabai berikut:

f₁(x) = 1/(1+ e^–x)

dengan turunan

f₁’(x) = f₁(x) (1- f₁(x))

berikut ini ilustrasi fungsi sigmoid biner:

Gambar 1. Ilustrasi fungsi sigmoid biner dengan range (0,1)

Fungsi Sigmoid Bipolar

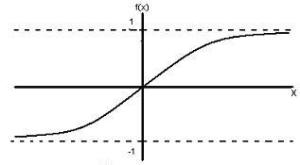
Fungsi sigmoid bipolar hampir sama dengan fungsi sigmoid biner, hanya saja output dari fungsi ini memiliki range antara 1 sampai -1. Definisi fungsi sigmoid bipolar adalah sebagai berikut:

f₂(x) = 2 f₂(x) -1

dengan turunan

f₂’(x) = ½ (1+ f₂(x)) (1- f₂(x))

Berikut ini adalah ilustrasi fungsi sigmoid bipolar:

Gambar 2. Ilustrasi fungsi sigmoid bipolar dengan range (-1,1)

Inti perhitungan pada algoritma berbasis jaringan adalah untuk mencari bobot terbaik dari contoh / sampel data yang sudah ada. Karena hasil pada contoh data sudah diketahui, maka nilai bobot akan dihitung berdasarkan nilai hasil yang sudah tersedia, sampai ditemukan nilai bobot terbaik yang paling banyak cocok apabila dihitungkan kembali pada data awal. Kemudian nilai bobot tersebut dapat digunakan untuk menghitung data lain yang tidak diketahui hasilnya.
Algoritma ini adalah variasi lain dari Algoritma JST (Jaringan Saraf Tiruan), dimana sistem pencarian matriks bobot yang umum digunakan adalah menggunakan PSO (Particle Swarm Optimization), Back-Propagation, dan EO (Evolutionary Optimization). Pada pembahasan kali ini akan digunakan teknik yang cukup sederhana yaitu Simplex Optimization.
Simplex Optimization bekerja dengan cara membentuk segitiga solusi yang dikatakan sebagai solusi terbaik – lainnya – terburuk. Pada setiap perhitungan, segitiga ini akan dihitung sehingga semakin mendekati solusi yang terbaik. Apabila segitiga ini digambar secara berurutan pada setiap perulangan, gerakan segitiga yang terjadi mirip dengan pola gerakan amoeba, oleh karena itu teknik ini juga disebut sebagai AMO (Amoeba Method Optimization).

Diasumsikan ada 8 data pelanggan yang sudah diketahui datanya, yaitu Pelanggan A,B,C,D,E,F,G,H
Masing-masing pelanggan memiliki kriteria, yaitu umur, jenis kelamin, skor kepribadian, dan memiliki nilai hasil yaitu Diterima / Ditolak
Diasumsikan 8 data tersebut adalah sebagai berikut:

Pelanggan	Umur	Jenis Kelamin	Skor Kepribadian	Hasil
Pelanggan A	44	Laki-laki	3.55	Diterima
Pelanggan B	52	Perempuan	4.71	Diterima
Pelanggan C	60	Perempuan	6.56	Ditolak
Pelanggan D	56	Laki-laki	6.8	Ditolak
Pelanggan E	51	Laki-laki	6.94	Ditolak
Pelanggan F	46	Perempuan	6.52	Ditolak
Pelanggan G	48	Laki-laki	4.25	Diterima
Pelanggan H	58	Perempuan	5.71	Diterima

Contoh data pelanggan awal adalah sebagai berikut:
Untuk Kriteria Jenis Kelamin:
Laki-laki dilambangkan dengan angka -1
Perempuan dilambangkan dengan angka +1
Untuk kriteria Nilai Hasil:
Terdapat 2 kolom untuk merepresentasikan kondisi Diterima dan Ditolak
Jika kondisi Diterima, maka inputan data kolom adalah 1, 0
Jika kondisi Ditolak, maka inputan data kolom adalah 0, 1

Dim data(9)() As Double
data(0) = New Double() {44, -1, 3.55, 1, 0}
data(1) = New Double() {52, +1, 4.71, 1, 0}
data(2) = New Double() {60, +1, 6.56, 0, 1}
data(3) = New Double() {56, -1, 6.8, 0, 1}
data(4) = New Double() {51, -1, 6.94, 0, 1}
data(5) = New Double() {46, +1, 6.52, 0, 1}
data(6) = New Double() {48, -1, 4.25, 1, 0}
data(7) = New Double() {58, +1, 5.71, 1, 0}

Selanjutnya ada 2 orang pelanggan baru yang mengajukan kredit sepeda motor
Maka tentukan pelanggan ini nantinya akan termasuk dalam kelompok Diterima / Ditolak
Diasumsikan data awalnya adalah sebagai berikut:

Pelanggan	Umur	Jenis Kelamin	Skor Kepribadian
Pelanggan I	47	Perempuan	6.05
Pelanggan J	52	Laki-Laki	5

Contoh data pelanggan baru adalah sebagai berikut:
Untuk kriteria Nilai Hasil:
Terdapat 2 kolom untuk merepresentasikan kondisi Diterima dan Ditolak
Karena belum diketahui nilai hasilnya, maka semua inputan data adalah -1, -1

data(8) = New Double() {47, +1, 6.05, -1, -1}
data(9) = New Double() {52, -1, 5, -1, -1}

Langkah-langkah penggunaan algoritma ini adalah

1. Lakukan normalisasi data untuk kriteria Umur dan Skor Kepribadian
Penjelasan lebih lanjut dapat dilihat pada penjelasan skrip dibawah ini (poin 1a – 1c)

1a. Hitung nilai rata-rata tiap-tiap kolom
yaitu dengan rumus: jumlah semua data dibagi dengan jumlah datanya

Dim total As Double = 0.0
For r = 0 To jumlahBaris - 1
 total += data(r)(c)
Next r
Dim rata2 As Double = total / jumlahBaris
hasil(0)(c) = rata2

1b. Hitung nilai standar deviasi tiap-tiap kolom
yaitu dengan rumus: akar dari ((kuadrat dari (jumlah dari (data – rata-rata))) / jumlah data)

Dim totalKuadrat As Double = 0.0
For r = 0 To jumlahBaris - 1
 totalKuadrat += (data(r)(c) - rata2) * (data(r)(c) - rata2)
Next r
Dim stdDev As Double = Math.Sqrt(totalKuadrat / jumlahBaris)
hasil(1)(c) = stdDev

1c. Normalisasi data dihitung dengan rumus (data – (rata-rata kriteria tersebut)) / standar deviasi kriteria tersebut

For c = 0 To kolom.Length - 1
 Dim j As Integer = kolom(c)
 Dim rata2 As Double = hasil(0)(j)
 Dim stdDev As Double = hasil(1)(j)

 For i = 0 To jumlahBaris - 1
  data(i)(j) = (data(i)(j) - rata2) / stdDev
 Next i
Next c

2. Tentukan skema awal untuk algoritma ini.
Algoritma ini dapat digunakan untuk melakukan perhitungan yang memiliki banyak input dan menghasilkan banyak output
Diasumsikan dalam kasus ini, skema yang digunakan adalah 3 – 4 – 2, dimana:

3 adalah jumlah saraf input, karena ada 3 kriteria awal, yaitu Umur, Jenis Kelamin, dan Skor Kepribadian
4 adalah jumlah saraf tersembunyi yang digunakan. Jumlah saraf tersembunyi harus lebih dari jumlah saraf input

dalam kasus ini bisa lebih dari 4, tetapi hanya digunakan 4 saja untuk mempercepat perhitungan

2 adalah jumlah saraf output, Karena kriteria nilai hasil bergantung pada nilai 2 kolom, yaitu 1,0 jika diterima dan 0,1 jika ditolak

Const jumlahSarafInput As Integer = 3
Const jumlahSarafTersembunyi As Integer = 4
Const jumlahSarafOutput As Integer = 2
Dim jst As New JaringanSaraf(jumlahSarafInput, jumlahSarafTersembunyi, jumlahSarafOutput)

* Diperlukan sebuah class untuk menyimpan semua matriks data untuk digunakan dalam perhitungan algoritma ini. Class ini dinamakan class JaringanSaraf. Deklarasi awal untuk setiap pengisian data adalah sebagai berikut

Public Class JaringanSaraf
    Private rnd As Random

    Private jumlahSarafInput As Integer
    Private jumlahSarafTersembunyi As Integer
    Private jumlahSarafOutput As Integer

    Private inputs As Double()

    'Matriks data untuk perhitungan jaringan saraf input-tersembunyi
    Private ihBobot As Double()()                   'Nilai bobot pada jaringan saraf input-tersembunyi
    Private hBias As Double()                       'Nilai bias pada jaringan saraf tersembunyi
    Private hOutput As Double()                     'Nilai output sementara pada jaringan saraf tersembunyi

    'Matriks data untuk perhitungan jaringan saraf tersembunyi-output
    Private hoBobot As Double()()                   'Nilai bobot pada jaringan tersembunyi-output
    Private oBias As Double()                       'Nilai bias pada jaringan saraf output

    Private outputs As Double()

    Public Sub New(jumlahSarafInput As Integer, jumlahSarafTersembunyi As Integer, jumlahSarafOutput As Integer)
        rnd = New Random(0)
        Me.jumlahSarafInput = jumlahSarafInput
        Me.jumlahSarafTersembunyi = jumlahSarafTersembunyi
        Me.jumlahSarafOutput = jumlahSarafOutput

        Me.inputs = New Double(jumlahSarafInput - 1) {}

        Dim ihBobot As Double()() = New Double(jumlahSarafInput - 1)() {}
        For r As Integer = 0 To ihBobot.Length - 1
            ihBobot(r) = New Double(jumlahSarafTersembunyi - 1) {}
        Next
        Me.ihBobot = ihBobot
        Me.hBias = New Double(jumlahSarafTersembunyi - 1) {}
        Me.hOutput = New Double(jumlahSarafTersembunyi - 1) {}

        Dim hoBobot As Double()() = New Double(jumlahSarafTersembunyi - 1)() {}
        For r As Integer = 0 To hoBobot.Length - 1
            hoBobot(r) = New Double(jumlahSarafOutput - 1) {}
        Next
        Me.hoBobot = hoBobot
        Me.oBias = New Double(jumlahSarafOutput - 1) {}

        Me.outputs = New Double(jumlahSarafOutput - 1) {}
    End Sub
 
 . . .
End Class

3. Sebelum masuk ke dalam fungsi utama perhitungan, ada beberapa parameter yang perlu diperhatikan, yaitu:

3a. Tentukan Jumlah maksimal Epoch
Epoch adalah banyak perulangan yang dilakukan dalam 1 kali proses pembelajaran
Diasumsikan dalam kasus ini jumlah maksimal Epoch adalah 100

Const maksEpoch As Integer = 100

4. Lakukan proses pencarian nilai bobot dan bias terbaik
Metode yang digunakan adalah Simplex Optimization
Penjelasan lebih detail tentang fungsi ini dapat dilihat pada penjelasan skrip dibawah ini (poin 4a – 4i)

Dim bobotTerbaik As Double() = jst.Simplex(contohData, maksEpoch)
jst.setBobot(bobotTerbaik)

Memasuki perhitungan utama pada fungsi Simplex

* Inisialisasi jumlah bobot yang digunakan dalam perhitungan

jumlah nilai bobot pada jaringan saraf input-tersembunyi adalah jumlah saraf input * jumlah saraf tersembunyi (3 * 4 = 12 buah)
jumlah nilai bias pada jaringan saraf input-tersembunyi adalah jumlah saraf tersembunyi (4 buah)
jumlah nilai bobot pada jaringan saraf tersembunyi-output adalah jumlah saraf tersembunyi * jumlah saraf output (4 * 2 = 8 buah)
jumlah nilai bias pada jaringan saraf tersembunyi-output adalah jumlah saraf output (2 buah)

Sehingga, banyak data yang diperlukan adalah 12 + 4 + 8 + 2 = 26 buah data
Fungsi ini akan mencari data yang memiliki bobot terendah diantara semua data input, dan akan mengembalikan 26 buah data dengan susunan seperti diatas

Dim jumlahBobot As Integer = (Me.jumlahSarafInput * Me.jumlahSarafTersembunyi) + (Me.jumlahSarafTersembunyi * Me.jumlahSarafOutput) + Me.jumlahSarafTersembunyi + Me.jumlahSarafOutput

4a. Ambil 3 nilai acak untuk dijadikan sebagai solusi sementara, yaitu solusi terbaik, terburuk, lainnya
Untuk masing-masing nilai tersebut, hitung tingkat kesalahannya menggunakan teknik MSE (Mean Squared Error)
yaitu jumlah dari (kuadrat dari (hasil terhitung – hasil pada data awal)) / jumlah data

Dim solusi As Solution() = New Solution(2) {}
For i As Integer = 0 To 2
 solusi(i) = New Solution(jumlahBobot)
 solusi(i).bobot = CariSolusiAcak(jumlahBobot)
 solusi(i).nilaiKesalahan = MeanSquaredError(contohData, solusi(i).bobot)
Next

* Gunakan fungsi ini untuk menghitung tingkat kesalahan dari masing-masing data input
Hitung tingkat kesalahan nilai jawaban menggunakan teknik Mean Squared Error
dihitung dengan rumus jumlah dari (kuadrat dari (nilai jawaban – nilai hasil pada matriks data)) / jumlah data
Nilai jawaban yang baru bisa jadi mengembalikan nilai MSE yang lebih tinggi, sehingga nilai jawaban ini tidak bisa dipakai

Private Function MeanSquaredError(contohData As Double()(), bobot As Double()) As Double
Me.setBobot(bobot)

Dim contohDataKolomKriteria As Double() = New Double(jumlahSarafInput - 1) {}
Dim contohDataKolomHasil As Double() = New Double(jumlahSarafOutput - 1) {}

Dim hasil As Double = 0.0
For i As Integer = 0 To contohData.Length - 1
 Array.Copy(contohData(i), contohDataKolomKriteria, jumlahSarafInput)
 Array.Copy(contohData(i), jumlahSarafInput, contohDataKolomHasil, 0, jumlahSarafOutput)
 Dim dataKolomHasil As Double() = Me.ComputeOutputs(contohDataKolomKriteria)
 For j As Integer = 0 To dataKolomHasil.Length - 1
  hasil += ((dataKolomHasil(j) - contohDataKolomHasil(j)) * (dataKolomHasil(j) - contohDataKolomHasil(j)))
 Next
Next
Return hasil / contohData.Length
End Function

4b. Pada setiap perulangan,
Urutkan solusi berdasarkan tingkat kesalahan terendahnya, kemudian masukkan nilai bobot terbaik – lainnya – terburuk sesuai urutan yang ada

Array.Sort(solusi)
Dim bobotTerbaik As Double() = solusi(indeksSolusiTerbaik).bobot
Dim bobotLainnya As Double() = solusi(indeksSolusiLainnya).bobot
Dim bobotTerburuk As Double() = solusi(indeksSolusiTerburuk).bobot

4c. Cari nilai centroid, yaitu nilai tengah dari solusi lainnya ke solusi terbaik

Dim bobotCentroid As Double() = Centroid(bobotLainnya, bobotTerbaik)

* Gunakan fungsi ini untuk mencari nilai centroid

Private Function Centroid(bobotLainnya As Double(), bobotTerbaik As Double()) As Double()
 Dim jumlahBobot As Integer = bobotLainnya.Length
 Dim hasil As Double() = New Double(jumlahBobot - 1) {}
 For i As Integer = 0 To hasil.Length - 1
  hasil(i) = (bobotLainnya(i) + bobotTerbaik(i)) / 2.0
 Next
 Return hasil
End Function

4d. Cari nilai expanded, yaitu nilai centroid ditambah (nilai centroid – nilai terburuk) dikali 2
Kemudian hitung tingkat kesalahannya menggunakan teknik MSE (Mean Squared Error)
Jika nilai kesalahan expanded kurang dari nilai kesalahan terburuk, maka nilai expanded akan menggantikan nilai terburuk

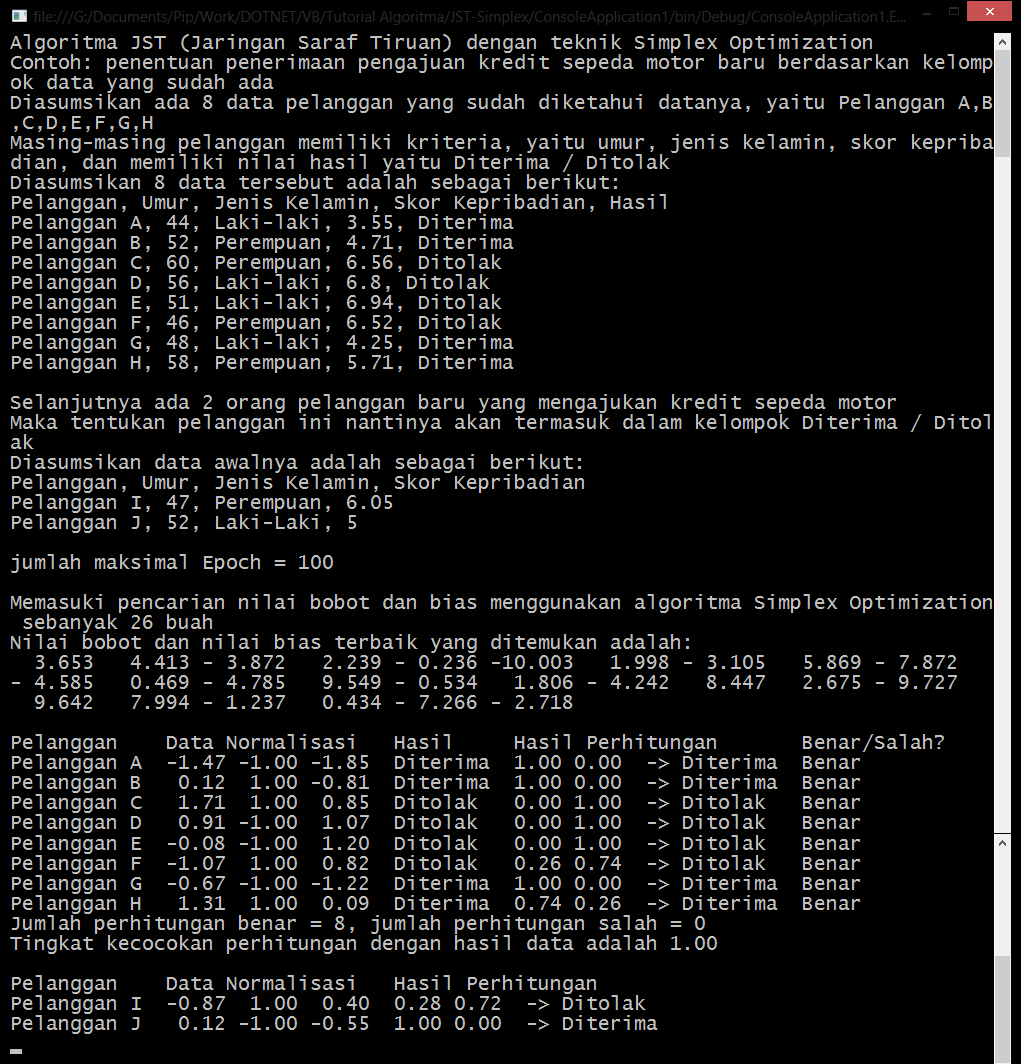
Dim bobotExpanded As Double() = Expanded(bobotCentroid, bobotTerburuk)
Dim nilaiKesalahanExpanded As Double = MeanSquaredError(contohData, bobotExpanded)
If nilaiKesalahanExpanded 

4e. Cari nilai reflected, yaitu nilai centroid ditambah (nilai centroid - nilai terburuk) dikali 1

Kemudian hitung tingkat kesalahannya menggunakan teknik MSE (Mean Squared Error)

Jika nilai kesalahan reflected kurang dari nilai kesalahan terburuk, maka nilai reflected akan menggantikan nilai terburuk
Dim bobotReflected As Double() = Reflected(bobotCentroid, bobotTerburuk)
Dim nilaiKesalahanReflected As Double = MeanSquaredError(contohData, bobotReflected)
If nilaiKesalahanReflected 

4f. Cari nilai contracted, yaitu nilai centroid ditambah (nilai centroid - nilai terburuk) dikali - 0.5

Kemudian hitung tingkat kesalahannya menggunakan teknik MSE (Mean Squared Error)

Jika nilai kesalahan contracted kurang dari nilai kesalahan terburuk, maka nilai contracted akan menggantikan nilai terburuk
Dim bobotContracted As Double() = Contracted(bobotCentroid, bobotTerburuk)
Dim nilaiKesalahanContracted As Double = MeanSquaredError(contohData, bobotContracted)
If nilaiKesalahanContracted 

Gunakan 3 fungsi dibawah ini untuk mencari nilai reflected, expanded, contracted

Ilustrasi singkat adalah sebagai berikut:
b----------x----------c----------y----------z

buruk-----------------centroid

Tarik garis lurus antara posisi terburuk dengan posisi centroid

Kemudian tambahkan garis terusan dari posisi centroid sepanjang jarak sebelumnnya

Posisi Expanded   berada pada posisi z, dengan jarak (centroid-buruk) * koefisien gamma, dalam contoh ini bernilai 2.0

Posisi Reflected  berada pada posisi y, dengan jarak (centroid-buruk) * koefisien alpha, dalam contoh ini bernilai 1.0

Posisi Contracted berada pada posisi x, dengan jarak (centroid-buruk) * koefisien beta, dalam contoh ini bernilai 0.5
'Gunakan fungsi ini untuk mencari nilai expanded
Private Function Expanded(Centroid As Double(), bobotTerburuk As Double()) As Double()
 Dim jumlahBobot As Integer = Centroid.Length
 Dim gamma As Double = 2.0
 Dim hasil As Double() = New Double(jumlahBobot - 1) {}
 For i As Integer = 0 To hasil.Length - 1
  hasil(i) = Centroid(i) + (gamma * (Centroid(i) - bobotTerburuk(i)))
 Next
 Return hasil
End Function

'Gunakan fungsi ini untuk mencari nilai reflected
Private Function Reflected(Centroid As Double(), bobotTerburuk As Double()) As Double()
 Dim jumlahBobot As Integer = Centroid.Length
 Dim alpha As Double = 1.0
 Dim hasil As Double() = New Double(jumlahBobot - 1) {}
 For i As Integer = 0 To hasil.Length - 1
  hasil(i) = Centroid(i) + (alpha * (Centroid(i) - bobotTerburuk(i)))
 Next
 Return hasil
End Function

'Gunakan fungsi ini untuk mencari nilai contracted
Private Function Contracted(Centroid As Double(), bobotTerburuk As Double()) As Double()
 Dim jumlahBobot As Integer = Centroid.Length
 Dim rho As Double = -0.5
 Dim hasil As Double() = New Double(jumlahBobot - 1) {}
 For i As Integer = 0 To hasil.Length - 1
  hasil(i) = Centroid(i) + (rho * (Centroid(i) - bobotTerburuk(i)))
 Next
 Return hasil
End Function


4g. Cari nilai acak lagi

Kemudian hitung tingkat kesalahannya menggunakan teknik MSE (Mean Squared Error)

Jika nilai kesalahannya kurang dari nilai kesalahan terburuk, maka nilai ini akan menggantikan nilai terburuk
Dim bobotSolusiAcak As Double() = CariSolusiAcak(jumlahBobot)
Dim nilaiKesalahanSolusiAcak As Double = MeanSquaredError(contohData, bobotSolusiAcak)
If nilaiKesalahanSolusiAcak 

4h. Jika nilai kesalahan dari posisi expanded - reflected - contracted - solusi acak tidak ada yang kurang dari nilai kesalahan solusi terburuk,

Maka hitung nilai solusi lainnya dan solusi terburuk yang baru.

4h1. Hitung nilai solusi terburuk yang baru, yaitu (nilai terburuk + nilai terbaik) dibagi 2

Kemudian hitung tingkat kesalahannya menggunakan teknik MSE (Mean Squared Error)
For j As Integer = 0 To jumlahBobot - 1
 bobotTerburuk(j) = (bobotTerburuk(j) + bobotTerbaik(j)) / 2.0
Next
solusi(indeksSolusiTerburuk).nilaiKesalahan = MeanSquaredError(contohData, bobotTerburuk)


4h2. Hitung nilai solusi lainnya yang baru, yaitu (nilai lainnya + nilai terbaik) dibagi 2

Kemudian hitung tingkat kesalahannya menggunakan teknik MSE (Mean Squared Error)
For j As Integer = 0 To jumlahBobot - 1
 bobotLainnya(j) = (bobotLainnya(j) + bobotTerbaik(j)) / 2.0
Next
solusi(indeksSolusiLainnya).nilaiKesalahan = MeanSquaredError(contohData, bobotLainnya)


4i. Dapatkan solusi terbaik, yaitu solusi pada indeks terbaik
Me.setBobot(solusi(indeksSolusiTerbaik).bobot)


* Gunakan fungsi ini untuk memasukkan matriks bobot awal kedalam 4 matriks data yaitu matriks ihBobot, hBias, hoBobot, oBias

ihBobot adalah matriks bobot pada jaringan saraf input-tersembunyi, dengan jumlah data = jumlah saraf input * jumlah saraf tersembunyi (3 * 4 = 12 buah)

hBias adalah matriks nilai bias pada jaringan saraf input-tersembunyi, dengan jumlah data = jumlah saraf tersembunyi (4 buah)

hoBobot adalah matriks bobot pada jaringan saraf tersembunyi-output, dengan jumlah data = jumlah saraf tersembunyi * jumlah saraf output (4 * 2 = 8 buah)

oBias adalah matriks nilai bias pada jaringan saraf tersembunyi-output, dengan jumlah data = jumlah saraf output (2 buah)
Public Sub setBobot(bobot As Double())
 Dim jumlahBobot As Integer = (jumlahSarafInput * jumlahSarafTersembunyi) + (jumlahSarafTersembunyi * jumlahSarafOutput) + jumlahSarafTersembunyi + jumlahSarafOutput
 If bobot.Length  jumlahBobot Then
  Throw New Exception("Pada fungsi SetBobotAwal, panjang matriks bobot: " & bobot.Length & " tidak sama dengan jumlah bobot yang seharusnya, yaitu " & jumlahBobot)
 End If

 Dim k As Integer = 0
 For i As Integer = 0 To jumlahSarafInput - 1
  For j As Integer = 0 To jumlahSarafTersembunyi - 1
   ihBobot(i)(j) = bobot(k)
   k += 1
  Next
 Next
 For i As Integer = 0 To jumlahSarafTersembunyi - 1
  hBias(i) = bobot(k)
  k += 1
 Next
 For i As Integer = 0 To jumlahSarafTersembunyi - 1
  For j As Integer = 0 To jumlahSarafOutput - 1
   hoBobot(i)(j) = bobot(k)
   k += 1
  Next
 Next
 For i As Integer = 0 To jumlahSarafOutput - 1
  oBias(i) = bobot(k)
  k += 1
 Next
End Sub


5. Lakukan perhitungan dari masing-masing contoh data menggunakan nilai bobot dan nilai bias yang sudah ditemukan

Penjelasan tentang fungsi ini akan dijelaskan pada perhitungan dibawah ini (poin 5a - 5g)
Dim output() As Double = jst.hitungNilaiOutput(input)


Memasuki perhitungan utama pada fungsi hitungNilaiOutput

5a. Beri nilai matriks input sesuai array input
For i = 0 To input.Length - 1
 Me.inputs(i) = input(i)
Next i


5b. Hitung matriks ihJumlahBobotDanBias dengan cara perkalian matriks antara matriks input dan matriks ihBobot
For j = 0 To jumlahSarafTersembunyi - 1
 For i = 0 To jumlahSarafInput - 1
  ihJumlahBobotDanBias(j) += Me.inputs(i) * ihBobot(i)(j)
 Next i
Next j


5c. Kemudian masukkan nilai bias pada matriks ihJumlahBobotDanBias
For i = 0 To jumlahSarafTersembunyi - 1
 ihJumlahBobotDanBias(i) += hBias(i)
Next i


5d. Hitung nilai output sementara dengan menggunakan fungsi HyperTan untuk masing-masing data pada matriks hJumlahBobotDanBias

Penjelasan tentang fungsi HyperTan akan dijelaskan pada perhitungan dibawah ini
For i As Integer = 0 To jumlahSarafTersembunyi - 1
 Me.hOutput(i) = HyperTan(hJumlahBobotDanBias(i))
Next


* Gunakan fungsi ini untuk menghitung nilai fungsi HyperTan (tanh)
Private Shared Function HyperTan(x As Double) As Double
 If x  20.0 Then
  Return 1.0
 Else
  Return Math.Tanh(x)
 End If
End Function


5e. Hitung matriks hoJumlahBobotDanBias dengan cara perkalian matriks antara matriks output sementara dan matriks hoBobot
For j = 0 To jumlahSarafOutput - 1
 For i = 0 To jumlahSarafTersembunyi - 1
  hoJumlahBobotDanBias(j) += hOutput(i) * hoBobot(i)(j)
 Next i
Next j


5f. Kemudian masukkan nilai bias pada matriks hoJumlahBobotDanBias
For i = 0 To jumlahSarafOutput - 1
 hoJumlahBobotDanBias(i) += oBias(i)
Next i


5g. Hitung nilai output akhir dengan menggunakan fungsi Softmax untuk masing-masing data pada matriks hoJumlahBobotDanBias

Penjelasan tentang fungsi Softmax akan dijelaskan pada perhitungan dibawah ini (poin 5g1 - 5g3)
Dim hasil() As Double = Softmax(hoJumlahBobotDanBias)
hasil.CopyTo(Me.outputs, 0)
Return hasil


Memasuki perhitungan utama pada fungsi Softmax

5g1. Cari nilai maksimal data
Dim maksData As Double = hoJumlahBobotDanBias(0)
For i = 0 To hoJumlahBobotDanBias.Length - 1
 If hoJumlahBobotDanBias(i) > maksData Then
  maksData = hoJumlahBobotDanBias(i)
 End If
Next i


5g2. Cari nilai skala
Dim skala As Double = 0.0
For i = 0 To hoJumlahBobotDanBias.Length - 1
 skala += Math.Exp(hoJumlahBobotDanBias(i) - maksData)
Next i


5g3. Hitung hasil akhir

Sehingga semua jumlah bobot pada parameter matriks hoJumlahBobotDanBias akan bernilai 1
Dim hasil(hoJumlahBobotDanBias.Length - 1) As Double
For i = 0 To hoJumlahBobotDanBias.Length - 1
 hasil(i) = Math.Exp(hoJumlahBobotDanBias(i) - maksData) / skala
Next i


6. Jika nilai output bernilai kurang dari 0.5 maka pelanggan tersebut memiliki nilai hasil Ditolak

Jika nilai output bernilai lebih dari 0.5 maka pelanggan tersebut memiliki nilai hasil Diterima

Kemudian bandingkan nilai output dengan nilai hasil pada contoh data

Jika hasilnya sudah sama, maka catat data ini kedalam jumlah data benar

Jika hasilnya tidak sama, maka catat data ini kedalam jumlah data salah
If output(0)  Ditolak   ")
 If contohData(i)(jumlahKolom - 2)  contohData(i)(jumlahKolom - 1) Then
  jumlahSalah += 1
  Console.WriteLine("Salah")
 End If
Else
 Console.Write("-> Diterima  ")
 If contohData(i)(jumlahKolom - 2)  contohData(i)(jumlahKolom - 1) Then
  jumlahBenar += 1
  Console.WriteLine("Benar")
 End If
End If


7. Catat tingkat kecocokan perhitungan data dengan hasil awal pada data

Langkah ini tidak wajib, hanya untuk mengetahui seberapa besar tingkat kecocokan perhitungan untuk data baru yang akan dihitung selanjutnya
Console.WriteLine("Jumlah perhitungan benar = " & jumlahBenar & ", jumlah perhitungan salah = " & jumlahSalah)
Console.WriteLine("Tingkat kecocokan perhitungan dengan hasil data adalah " & (jumlahBenar / (jumlahBenar + jumlahSalah)).ToString("F2"))


8. Lakukan perhitungan yang sama (poin 5 dan 6) untuk masing-masing data baru
For i As Integer = 0 To dataBaru.Length - 1
 Console.Write("Pelanggan " & Chr(i + 65 + 8) & "  ")

 Dim input(jumlahKolom - 3) As Double
 Array.Copy(dataBaru(i), input, jumlahKolom - 2)
 For j = 0 To input.Length - 1
  Console.Write(IIf(input(j) >= 0, " ", "") & input(j).ToString("F2") & " ")
 Next j
 Console.Write(" ")

 Dim output() As Double = jst.hitungNilaiOutput(input)
 For j = 0 To output.Length - 1
  Console.Write(output(j).ToString("F2") & " ")
 Next j
 Console.Write(" ")

 If output(0)  Ditolak ")
 Else
  Console.Write("-> Diterima")
 End If
 Console.WriteLine("")
Next


* Agar dapat menjalankan fungsi Simplex diatas, maka diperlukan sebuah Class Solution untuk menampung semua data bobot dan nilai kesalahan solusi tersebut. Deklarasi Class Solution adalah sebagai berikut:
Private Class Solution
 Implements IComparable(Of Solution)
 Public bobot As Double()
 Public nilaiKesalahan As Double

 Public Sub New(jumlahBobot As Integer)
  Me.bobot = New Double(jumlahBobot - 1) {}
  Me.nilaiKesalahan = 0.0
 End Sub

 'Fungsi untuk mengurutkan nilai kesalahan dari yang terendah (terbaik) ke tertinggi (terburuk)
 Public Function CompareTo(other As Solution) As Integer Implements IComparable(Of Solution).CompareTo
  If Me.nilaiKesalahan  other.nilaiKesalahan Then
   Return 1
  Else
   Return 0
  End If
 End Function
End Class




Hasil akhir adalah: (klik untuk perbesar gambar)

sumber:

https://jalanwaktu.wordpress.com/jaringan-syaraf-tiruan/

https://piptools.net/algoritma-jst-jaringan-saraf-tiruan-dengan-teknik-simplex-optimization/amp/

#JustRandomBlog

Thursday, January 3, 2019

Algoritma Jaringan Saraf Buatan

1. Pengertian Jaringan Syaraf Tiruan

2. Konsep Dasar Jaringan Syaraf Tiruan

1. Pengertian Jaringan Syaraf Tiruan

2. Konsep Dasar Jaringan Syaraf Tiruan

3. Karakteristik Jaringan Syaraf Tiruan

Langkah-langkah penggunaan algoritma ini adalah

Hasil akhir adalah: (klik untuk perbesar gambar)

sumber:

https://jalanwaktu.wordpress.com/jaringan-syaraf-tiruan/